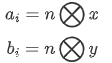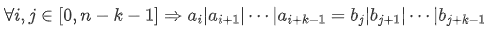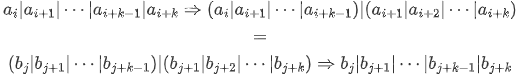10 条说说
在.clangd上添加一下代码即可，关键点在于 -mabi=lp64：
CompileFlags: Remove: [-femit-struct-debug-baseonly, -fconserve-stack, -fno-omit-frame-pointer, -fno-var-tracking-assignments, -fno-var-tracking-assignments, -fmin-function-alignment=4, -fno-allow-store-data-races, -mabi=lp64]
Windows 跳过联网设置，使用
shift-F10
打开命令行，然后输入
OOBE\BYPASSNRO
跳过联网
查看电池报告：
powercfg \batteryreport
题目描述：
给定一个数组 $A$ ，找到一个数 $x$ ，使得数组 $A$ 中所有长度大于 $2$ 的子数组 $A’$ 的最大值严格大于 $x$，求 $x$ 可取的最大值。
数据约束：
$2 \le n \le 5 \times 10^5$ ，$1 \le a_i \le 10^9$
解题思路：
找到所有长度等于 $2$ 的子数组的最大值的最小值 $m$ ，则 $x = m – 1$。
复杂度：时间复杂度 $O(n)$ ，空间复杂度 $O(n)$
题目描述：
给定两个数 $x, y$ ，现有两个无限长度的数组 $A, B$ 。两个数组的构造方式如下：
求这两个数组的公共最长字串的最大长度。
数据约束：
$1 \le x, y \le 10^9$
解题思路：
异或就是相同为 $0$ ，不同为 $1$ 。那么最长公共字串的长度就是 $x, y$ 相同最低为的长度所能表示的二进制数的最大值。
复杂度：时间复杂度 $O(\log x)$ ，空间复杂度 $O(1)$
题目描述：
给定一个数组 $K$ ，长度为 $n$ 。要求构造一个数组 $A$ ，长度同样为 $n$ 。我们定义 $S = \sum_{i=1}^{n} a_i$ ，现要求 $\forall i \in[1, n]$ ，都有 $a_i \times k_i > S$ 。请构造这样的一个数组 $A$ 。
数据约束：
$1 \le n \le 50$ ，$2 \le k \le 20$
解题思路：
我们假设一个数 $x$， 每个数 $a_i = \frac{x}{ki}$ ，那么我们只需要满足 $\sum{i = 1}^{n} \frac{x}{k_i} < x$ 即可，如果不能满足该不等式，就不存在这么一个数组 $A$ 。对于这个数 $x$ ，我们可以选择数组 $K$ 的最小公倍数。
复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$
题目描述：
给定两个数 $n, k$ ，并提供一个字符串 $S$ ，这个字符串仅有 $0, 1$ 组成，且长度为 $n$ 。现需要对数组进行一下操作：
如果得到的字符串 $S”$ 满足以下条件：
我们称这个字符串是符合要求的。
求满足要求的 $p$ 值。（有可能有多个值，只需要输出一种即可）
数据约束：
$1 \le k \le n$ ，$2 \le n \le 2 \times 10^5$
解题思路：
可以推导发现，最终生成的字符串的形式是以连续 $k$ 个的 $0, 1$ 交替出现的序列，最后一组不一定要满足 $k$ 个。
我们维护两个数组：$dp_l[0/1][i]$ 表示以 $i$ 位置结尾的以 $0, 1$ 结尾左侧满足上述条件的连续 $k$ 个的组数；$dp_r[0/1][i]$ 表示以 $i$ 位置结尾右侧以 $0, 1$ 结尾左侧满足上述条件的连续 $k$ 个的组数。
遍历每一个位置 $p$ ，在右侧可以找到一个符合规定的最大长度，有可能会剩余一个不满足条件的子串，且这个子串长度必然小于 $k$ ，大于等于 $k$ 就不满足要求。既然长度不够，我们可以从 $p$ 的左侧借用一点子串来填充剩余部分。借用部分必须和剩余部分相同。
借用之后，我们在借用的左侧，寻找到最长符合要求的子串，此时也可能会剩余一个子串，且这个子串长度必然小于 $k$ ，大于等于 $k$ 就不满足要求。左侧剩余部分必须相同，且和符合部分进行有效衔接。
需要提升效率的地方就是查询这些符合规定的最大长度，此时就可以使用前面提到的 $dp$ 数组。又因为需要翻转，所以左侧是维护一个向左查询的数组，右侧是维护一个向右查询的数组，这就是为什么要两个 $dp$ 数组的原因。
这个题目的细节非常的多，这里我主要是少考虑了这两种情况，右侧符合规定的最大长度为 $0$ ，以及 $k = n$ 的情况。
复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$
题目描述：
我以另一种方式描述一下题目。你共有 $n$ 次机会，每次机会你可以进行 $+1$ 操作或者是 $-1$ 操作。请问 $n$ 次操作之后能否得到数字 $m$ 。
数据约束：
$1 \le n, m \le 100$
解题思路：
初中学习的二元一次方程组，有正整数解就可以。
复杂度：$O(1)$ 。
题目描述：
给定一个数 $x$ ，生成一个由 -1 和 0 和 1 构成数组 $A$ 。数组 $A$ 的要求如下：
数据约束：
$1 \le x \le 2^{30}$
解题思路：
很明显，第一条约束其实就是一个数的二进制表示法（不考虑 -1）。所有，先吧 $x$ 的二进制表示数组给求出来。
那么，第二跳约束就是数组中不能有连续的非零数出现。对于一个数的二进制表示来说，就是不能有连续的 1 出现。那么问题转化为，怎么对连续的 1 进行处理？
我们考虑一下二进制序列 ...01110... ，右侧为低位。如果我们对示例中最右侧的 1 进行 +1 操作，则会得到 ...10000... ，连续的 1 就消除了。又因为我们加了一个 1，所以我们也需要进行减 1 操作，即 ...100(-1)0... 。此时，满足了题目要求。
那么解法就是，从 $x$ 的二进制数最低位开始扫描，若遇到连续的 1 ，就进行上述操作，直到没有连续的 1 为止。
复杂度：时间复杂度 $O(\log x)$ ，空间复杂度：$O(\log x)$ 。
题目描述：
一个长度为 $n$ 的数组 $A$ ，我们规定特殊子数组为：该数组是 $A$ 的子数组，且该数组的最小公倍数未在数组 $A$ 中出现。
求数组 $A$ 中符合要求的特殊子数组的最长长度。
数据约束：
$1 \le n \le 2000$ ，$1 \le a_i \le 10^9$
解题思路：
开始没有思路，往动态规划想了。受了一点题解的启发，主要是这个发现：数组 $A$ 的最小公倍数的大于等于数组的最大值。
如果数组 $A$ 的最小公倍数大于了数组的最大值，则答案就是 $n$ 。否则，数组中所有数字都是数组最大值的因数。那么，我们遍历最大值的每一个因数 $d$ ，当 $d$ 不存在与数组 $A$ 中时，寻找数组 $A$ 中所有为 $d$ 的因数的数组成一个数组。如果得到的新数组的最小公倍数刚好等于 $d$ ，这个数组就是合法的。最后答案就是所有合法数组的长度的最大值。
复杂度：时间复杂度 $O(\sqrt{C} + d(C)^2 \times \log C)$ ，空间复杂度 $O(n)$ 。
题目描述：
三个人下棋，两个人一回合。在一个回合中，赢的一方得 2 分，输的一方不得分，平局两方各得 1 分。
现在已知三个人的得分情况，求出在得分情况下，可能的最大平局次数是多少？如果得分情况不合法，输出 -1。
数据范围：
$1 \le t \le 500$，$0 \le p_1 \le p_2 \le p_3 \le 30$
解题思路：
先考虑合不合法的情况。通过分析可以得出，不管是不是平局，最后所有人的得分之和都会增加 2。故可以得出规律，如果三位的得分之后不是偶数，就是不合法的情况，输出 -1。
那么合法的时候就会有这两种情况：
对于第一种情况，$p1, p_2$ 的得分都可以是平局产生的，产生的方式是和 $p_3$ 对局，所以答案就是 $p_1 + p_2$。对于第二种情况 $p_1,p_2$ 不可能全部得分都来自于和 $p_3$ 的对局。所以，需要 $p_1$ 和 $p_2$ 对局产生一些平局的分数。通过分析可以得到 $p1 + p_2 – p_3$ 必为偶数，而且除以 2 以后必然小于 $p_1$。所以，将多余的分数用于 $p_1$ 和 $p_2$ 打平局是可能的。总结，所有分数都可以用来打平局，故答案是 $\frac{p_1 + p_2 + p_3}{2}$ 。
复杂度：时间复杂度 $O(1)$ ，空间复杂度 $O(1)$ 。
题目描述：
题目定义了一个概念，叫孤独数组 $A$ 。定义如下：
假设数组的长度为 $n$，如果
则我们称 $A$ 为 $k$ 维孤独数组。
现给出一个特殊构造的数组，要求找出该数组 $k$ 可以取的最小值。
数据范围：
$1 \le t \le 10^4$，$1 \le n \le 10^5$
解题思路：
看到这个数据范围，就需要考虑 $O(n \log n)$ 的算法了。对于位运算的题目，就要考虑位拆解求解。对于这种区间值的问题，可以先维护一个前缀和。由于是或运算，我们只需要维护区间内有无 1 出现就行。看到最小值，就可以考虑是否可以二分求解。
可以发现，如果该数组 $A$ 为 $k$ 维孤独数组，那么必然是 $k + 1$ 维孤独数组。证明如下：
所以，二分解法是成立的。
复杂度：时间复杂度 $O(n \log n)$，空间复杂度 $O(n)$ 。
题目描述：
一共有 $n$ 道题目，每道题目的实际难度为 $a_i$，期望难度为 $b_i$。初始状态下，保证 $a_i$ 和 $b_i$ 严格递增，即有序的。
现在对这套题目难度，需要满足 $\forall i \in [1, n] \Rightarrow a_i \leq b_i$ 。如果不能满足这个要求，你可以删除最后一道题目，然后插入新的题目，重新排序后满足该要求即可。
问最少需要删除多少个题目？
数据约束：
$1 \leq n \leq 100$ ；$1 \leq a_i \leq 10^9$；$1 \leq b_i \leq 10^9$ 。
解题思路：
如果我们要删除题目，并插入新的题目，那么新的题目的难度可以是小于所有期望题目难度的；此时，删除题目相当于将题目往后平移一位。
如果 $a_i \leq b_i$，那么 $\forall j \in [1, i – 1] \Rightarrow a_j \leq b_i$ 。我们可以从后向前遍历，如果 $a_i > b_i$，则弹出 $a_i$，直到满足 $a_i \leq b_i$。那么总共弹出的次数就是最少需要删除题目的个数。
复杂度：时间复杂度 $O(n)$ ，空间复杂度 $O(1)$ 。
题目描述：
一共有 $n$ 个硬币排成一圈，它们不是朝上就是朝下。Alice 和 Bob 轮流玩游戏，Alice 先手。游戏规则，取走一枚面朝上的硬币，并翻转相邻的硬币（如果只剩两枚则不翻转）。如果当前玩家没有硬币可取，则输，另一位玩家赢。
问给定布局下，Alice 是否能赢。
数据约束：
$1 \leq n \leq 100$ 。
解题思路：
我们以中间的可取为例，共有以下几种情况：
UUU：取走后变成 DD，U 减少 3 枚。UUD：取走后变成 DU，U 减少 1 枚。DUU：取走后变成 UD，U 减少 1 枚。DUD：取走后变成 UU，U 增加 1 枚。可以发现，U 的个数都是以奇数个进行增减的。如果先手为奇数，最后一定会赢。
复杂度：时间复杂度 $O(n)$ ，空间复杂度 $O(1)$ 。
题目描述：
一共有 $n$ 中数字 $[1, n]$ ，每个数字 $i$ 有 $a_i$ 。你可以在此基础上增加 $k$ 个数字，数值由你决定，范围为 $[1, n]$ 。$k$ 次机会必须全部使用。
将新的数组进行重组，使其子数组中，为 $n$ 的全排列的个数最大。问这个最大的个数是多少。
数据约束：
$1 \leq n \leq 2 \times 10^5$ ；$0 \leq k \leq 10^{12}$ 。
$1 \leq a_i \leq 10^{12}$ 。
解题思路：
要想使得重新排列的数组的是 $n$ 的全排列子数组的个数最大，数组的排列应该类似于 1, 2, 3, ... , n - 1. n, 1, 2, 3, ...，即每连续 $n$ 个数 $[1, n]$ 都出现一次。假设这样的数组长度为 $l$，则全排列的子数组个数为 $l – n + 1$ 。
有多少个完整的全排列受限于最少的数的个数（木桶效应）。既然我们要是全排列的个数最大，就要将 $k$ 花费在数量最少的数上面，很容易就能想到时间复杂度为 $O(k)$ 的算法；但是，时间不允许。
要找到 $k$ 次操作后 $a_i$ 的最小值，我们二分查找在 $k$ 允许的情况下，这个最小值的最大值。即 $k$ 次操作之后，数组的最小值为 $m$ 。此时的时间复杂度就降为了 $O(\log k)$ 。 $k$ 的剩余次数，均匀的分到这些最小值上。
最后可以得到的连续全排列数组长度为
又因为
表达式再减去 $n – 1$，最后化简得到子数组为 $n$ 的全排列的个数为
复杂度：时间复杂度 $O(n\log k)$，空间复杂度 $O(1)$ 。
题目描述：
数组 nums1 中的每个元素都与变量 x 所表示的整数相加。如果 x 为负数，则表现为元素值的减少。
在与 x 相加后，nums1 和 nums2 相等 。当两个数组中包含相同的整数，并且这些整数出现的频次相同时，两个数组 相等 。
返回整数 x 。
数据约束：
数组大小 $n \le 100$；数据大小 $0 \le a_i \le 1000$。
解题思路：
数据范围很小，基本随便暴力。既然数据是定制化的，那么将两个数组排序后，下标相同的位置必然是一一对应的。再取一个特殊情况，两个数组的最小值，也是对应关系。那么答案就是这两个最小值的差值。
复杂度：时间复杂度 $O(n)$，空间复杂度 $O(1)$。
题目描述：
给你两个整数数组 nums1 和 nums2。
从 nums1 中移除两个元素，并且所有其他元素都与变量 x 所表示的整数相加。如果 x 为负数，则表现为元素值的减少。
执行上述操作后，nums1 和 nums2 相等 。当两个数组中包含相同的整数，并且这些整数出现的频次相同时，两个数组 相等 。
返回能够实现数组相等的 最小 整数 x 。
数据约束：
数组大小 $3 \le n \le 200$；数据大小 $0 \le a_i \le 1000$。
解题思路：
题目数组 1 要进行删减操作，而数组 2 并不需要。我们可以把题目反过来，在数组 2 上最大可以加多少，使其可以在数组 1 中找到与之对应的数（不重复）。答案范围肯定在 $-1000 \le ans \le 1000$，不妨对该区间的答案一一尝试，直到找到答案为止。
复杂度：时间复杂度 $O(\alpha n)$；空间复杂度 $O(\log n)$，维护每个数据出现的次数便于做比较。
题目描述：
给你两个整数 n 和 x 。你需要构造一个长度为 n 的 正整数 数组 nums ，对于所有 0 <= i < n - 1 ，满足 nums[i + 1] 大于 nums[i] ，并且数组 nums 中所有元素的按位 AND 运算结果为 x 。
返回 nums[n - 1] 可能的 最小 值。
数据约束：
$0 \le n, x \le 10^8$。
解题思路：
既然所有数据的按位与运算的结果要等于 $x$，那么所有数据在 $x$ 的比特位为 1 的位置上都必须为 1。那可以修改的空间就剩其余不是 1 的位置，抛去所有为 1 的位置，剩下位置进行填数，是数组严格递增。很明显，就是填 0,1,2,3,4……，直到填到 n – 1 为止。
那么做法就是，将 $n – 1$ 的二进制数嵌入到 $x$ 的二进制数不为 1 的地方。
复杂度：时间复杂度和空间复杂度都很小。
这场周赛是由【衍复投资】主办的，很偏数论，所以只做了两道题。
题目描述：
给你一个字符串 s，表示一个 12 小时制的时间格式，其中一些数字（可能没有）被 "?" 替换。
12 小时制时间格式为 "HH:MM" ，其中 HH 的取值范围为 00 至 11，MM 的取值范围为 00 至 59。最早的时间为 00:00，最晚的时间为 11:59。
你需要将 s 中的 所有 "?" 字符替换为数字，使得结果字符串代表的时间是一个 有效 的 12 小时制时间，并且是可能的 最晚 时间。
返回结果字符串。
数据约束：无
解题思路：
贪心。但是有点坑。对于分钟，确实可以贪心，两位数尽可能去最大；对于小时，不能这么干了（因为这个 WA 了两发），小时的取值范围是 0~11，不能认为 11 就是最大的，有可能是 0? 的形式，在个形式下，09 才是最大的。还有一种情况是 ?3，不可以取 13，超过了可以表示的时间的范围。
所以，对于小时，我们分成以下几种情况：
??：可以直接取 11。?1：第 2 位为 1 或者是 0。这种情况下，第 1 位可以取 1 而使其最大。?2：第 2 位是 2 以上的的数，这种情况下，第 1 位只能取 0。0?：第 2 位取 9。1?：第 2 位取 1。?：取原数。复杂度：时间复杂度 $O(1)$。
题目描述：
给你一个整数数组 nums。
返回两个（不一定不同的）素数在 nums 中 下标 的 最大距离。
数据约束：
数组大小 $n \leq 3 \times 10^5$；每个数值的大小 $nums_i \leq 100$。
解题思路：
最后结果为最右边的下标，和最左边的下标的差值。
筛素数的方法
- 埃氏筛
考虑这样一件事情：对于任意一个大于
的正整数
如果我们从小到大考虑每个数，然后同时把当前这个数的所有（比自己大的）倍数记为合数，那么运行结束的时候没有被标记的数就是素数了。
时间复杂度：$O(n \log \log n)$。
- 线性筛
vectorpri; bool not_prime[N]; void pre(int n) { for (int i = 2; i <= n; ++i) { if (!not_prime[i]) { pri.push_back(i); } for (int pri_j : pri) { if (i * pri_j > n) break; not_prime[i * pri_j] = true; if (i % pri_j == 0) { // i % pri_j == 0 // 换言之，i 之前被 pri_j 筛过了 // 由于 pri 里面质数是从小到大的，所以 i 乘上其他的质数的结果一定会被 // pri_j 的倍数筛掉，就不需要在这里先筛一次，所以这里直接 break // 掉就好了 break; } } } } 时间复杂度：$O(n)$
复杂度：时间复杂度 $O(n)$，空间复杂度 $O(1)$。
题目描述：
给你一个整数数组 coins 表示不同面额的硬币，另给你一个整数 k 。
你有无限量的每种面额的硬币。但是，你 不能 组合使用不同面额的硬币。
返回使用这些硬币能制造的 第 kth 小 金额。
数据约束：
硬币种数 $type \leq 15$；硬币面值 $coins_i \leq 25$；$k$ 在 32 位整型范围内。
解题思路：
转换一下题目的描述，就是将一组数的所有的倍数去重后排序，第 $k$ 小的数是什么？
虽然当时并没有想到怎么解决，但是想到了容斥。这些数的倍数中一定是有重复的，比如 [2, 3]，倍数中 6 就重复了。如何去除掉这个重复的数呢？容斥原理就可以解决这个问题。
容斥原理
设 U 中元素有 n 种不同的属性，而第 i 种属性称为
$$
\begin{aligned} \left|\bigcup_{i=1}^{n}Si\right|=&\sum{i}|Si|-\sum{i<j}|S_i\cap Sj|+\sum{i<j<k}|S_i\cap S_j\cap Sk|-\cdots\ &+(-1)^{m-1}\sum{ai<a{i+1} }\left|\bigcap{i=1}^{m}S{a_i}\right|+\cdots+(-1)^{n-1}|S_1\cap\cdots\cap Sn| \end{aligned}
$$
即
$$
\left|\bigcup{i=1}^{n}Si\right|=\sum{m=1}^n(-1)^{m-1}\sum_{ai<a{i+1} }\left|\bigcap{i=1}^mS{a_i}\right|
$$
用这些硬币，我们可以为每一个数列出它的所有倍数：
$$
a_i, 2a_i, 3a_i,\cdots
$$
那么重复的数字就是两两组合，三组合、四组合等的最小公倍数的倍数集。例如两两组合：
$$
lcm(a_i, a_j), 2lcm(a_i, a_j), 3lcm(a_i, a_j), \cdots
$$
这些数绝对在前面每个数的倍数列中重复了，需要容斥原理解决。然后就做不下去了，不知道如何求出这么多组合的最小公倍数。
忽视了数据范围，硬币种数 $type \leq 15$，故所有组合的种数就只有 $2^{15}$ 种（状态压缩），其实暴力枚举组合，求最小公倍数就好。
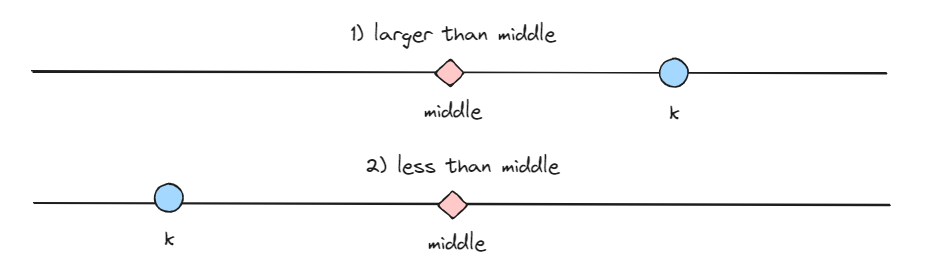
找到了所有的公倍数，我们就能知道一个数 $m$ 以内，有多少个公倍数出现。出现的次数 $cnt = \frac{m}{lcm}$，再通过容斥，去除掉重复的部分。这个时候，问题又转变了，找到一个最小的数，使得 $cnt_m \leq k$，这个最小的数，就是题目要要的数。此时可以二分求解了。
在
C++17中，可以直接使用lcm和gcd求解最小公倍数以及最大公因数。C++11可以直接__gcd求最大公因数，最小公因数可以 $lcm(a, b) = \frac{a \times b}{gcd(a, b)}$ 求解。
复杂度：时间复杂度 $O(\alpha 2^{t})$，空间复杂度 $O(1)$。
题目描述：返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。
数据约束：数组长度 $n \leq 50$。
解题思路：
遍历检查。维护两个数组，$incr[i]$ 表示以下标 $i$ 为结尾的最长严格递增的子数组；$desc[i]$ 表示以下标 $i$ 为结尾的最长严格递减子数组。转移公式如下：
$$
incr[i] = nums[i – 1] < nums[i] ? incr[i – 1] + 1 : 1
$$
$$
desc[i] = nums[i – 1] > nums[i] ? desc[i – 1] + 1 : 1
$$
最后答案为两个数组的最大值。
复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$。
题目描述：
给你一个字符串 s 和一个整数 k 。
定义函数 distance(s1, s2) ，用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离，即：
'a' 到 'z' 按 循环 顺序排列，对于区间 [0, n - 1] 中的 i ，计算所有「 s1[i] 和 s2[i] 之间 最小距离」的 和 。例如，distance("ab", "cd") == 4 ，且 distance("a", "z") == 1 。
你可以对字符串 s 执行 任意次 操作。在每次操作中，可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。
返回一个字符串，表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ，且满足 distance(s, t) <= k 。
数据约束：字符串长度 $n \leq 100$，$k \leq 200$。
解题思路：
贪心策略，毕竟要字典序最小。从第一个字符开始，从字符 a 开始尝试直到剩余操作次数满足将该字符进行修改，满足就进入到原字符串的下一位，直到修改次数用完为止。
复杂度：时间复杂度度 $O(n)$，空间复杂度 $O(n)$。
题目描述：
给你一个整数数组 nums 和一个 非负 整数 k 。
一次操作中，你可以选择任一下标 i ，然后将 nums[i] 加 1 或者减 1 。
请你返回将 nums 中位数 变为 k 所需要的 最少 操作次数。
一个数组的 中位数 指的是数组按 非递减 顺序排序后最中间的元素。如果数组长度为偶数，我们选择中间两个数的较大值为中位数。
数据约束：
数组长度 $n \leq 2e^5$，数据大小在 32 位整型范围内，$k$ 在 32 位整型范围内。
解题思路：
既然要操作次数最小，那么就只需要修改原数组中位数附近的数即可，因为这些数也离中位数的差值最小了。要找原数组的中位数，就需要对原数组进行排序。
要使 $k$ 成为中位数，就需要在排序后的原数组中找到比 $k$ 大的数的下标位置，可能有以下两种情况：
我们对其进行逐一讨论：
找到 $k$ 的位置可以遍历也可以二分。
复杂度：时间复杂度 $O(n \log n)$，空间复杂度 $O(n)$。
I come back！
上个服务器过期，没米续费，也没保存所有文章。现在有了超低配的free服务器，遂重搭，仅有部分之前的文章。