1 Contest Proposal
题目描述:
一共有 $n$ 道题目,每道题目的实际难度为 $a_i$,期望难度为 $b_i$。初始状态下,保证 $a_i$ 和 $b_i$ 严格递增,即有序的。
现在对这套题目难度,需要满足 $\forall i \in [1, n] \Rightarrow a_i \leq b_i$ 。如果不能满足这个要求,你可以删除最后一道题目,然后插入新的题目,重新排序后满足该要求即可。
问最少需要删除多少个题目?
数据约束:
$1 \leq n \leq 100$ ;$1 \leq a_i \leq 10^9$;$1 \leq b_i \leq 10^9$ 。
解题思路:
如果我们要删除题目,并插入新的题目,那么新的题目的难度可以是小于所有期望题目难度的;此时,删除题目相当于将题目往后平移一位。
如果 $a_i \leq b_i$,那么 $\forall j \in [1, i – 1] \Rightarrow a_j \leq b_i$ 。我们可以从后向前遍历,如果 $a_i > b_i$,则弹出 $a_i$,直到满足 $a_i \leq b_i$。那么总共弹出的次数就是最少需要删除题目的个数。
复杂度:时间复杂度 $O(n)$ ,空间复杂度 $O(1)$ 。
2 Coin Game
题目描述:
一共有 $n$ 个硬币排成一圈,它们不是朝上就是朝下。Alice 和 Bob 轮流玩游戏,Alice 先手。游戏规则,取走一枚面朝上的硬币,并翻转相邻的硬币(如果只剩两枚则不翻转)。如果当前玩家没有硬币可取,则输,另一位玩家赢。
问给定布局下,Alice 是否能赢。
数据约束:
$1 \leq n \leq 100$ 。
解题思路:
我们以中间的可取为例,共有以下几种情况:
UUU:取走后变成DD,U减少 3 枚。UUD:取走后变成DU,U减少 1 枚。DUU:取走后变成UD,U减少 1 枚。DUD:取走后变成UU,U增加 1 枚。
可以发现,U 的个数都是以奇数个进行增减的。如果先手为奇数,最后一定会赢。
复杂度:时间复杂度 $O(n)$ ,空间复杂度 $O(1)$ 。
3 Permutation Counting
题目描述:
一共有 $n$ 中数字 $[1, n]$ ,每个数字 $i$ 有 $a_i$ 。你可以在此基础上增加 $k$ 个数字,数值由你决定,范围为 $[1, n]$ 。$k$ 次机会必须全部使用。
将新的数组进行重组,使其子数组中,为 $n$ 的全排列的个数最大。问这个最大的个数是多少。
数据约束:
$1 \leq n \leq 2 \times 10^5$ ;$0 \leq k \leq 10^{12}$ 。
$1 \leq a_i \leq 10^{12}$ 。
解题思路:
要想使得重新排列的数组的是 $n$ 的全排列子数组的个数最大,数组的排列应该类似于 1, 2, 3, ... , n - 1. n, 1, 2, 3, ...,即每连续 $n$ 个数 $[1, n]$ 都出现一次。假设这样的数组长度为 $l$,则全排列的子数组个数为 $l – n + 1$ 。
有多少个完整的全排列受限于最少的数的个数(木桶效应)。既然我们要是全排列的个数最大,就要将 $k$ 花费在数量最少的数上面,很容易就能想到时间复杂度为 $O(k)$ 的算法;但是,时间不允许。
要找到 $k$ 次操作后 $a_i$ 的最小值,我们二分查找在 $k$ 允许的情况下,这个最小值的最大值。即 $k$ 次操作之后,数组的最小值为 $m$ 。此时的时间复杂度就降为了 $O(\log k)$ 。 $k$ 的剩余次数,均匀的分到这些最小值上。
最后可以得到的连续全排列数组长度为
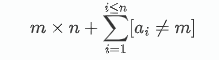
又因为
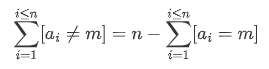
表达式再减去 $n – 1$,最后化简得到子数组为 $n$ 的全排列的个数为
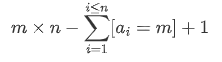
复杂度:时间复杂度 $O(n\log k)$,空间复杂度 $O(1)$ 。