1 Chess For Three
题目描述:
三个人下棋,两个人一回合。在一个回合中,赢的一方得 2 分,输的一方不得分,平局两方各得 1 分。
现在已知三个人的得分情况,求出在得分情况下,可能的最大平局次数是多少?如果得分情况不合法,输出 -1。
数据范围:
$1 \le t \le 500$,$0 \le p_1 \le p_2 \le p_3 \le 30$
解题思路:
先考虑合不合法的情况。通过分析可以得出,不管是不是平局,最后所有人的得分之和都会增加 2。故可以得出规律,如果三位的得分之后不是偶数,就是不合法的情况,输出 -1。
那么合法的时候就会有这两种情况:
- $p_1 + p_2 \le p_3$
- $p_1 + p_2 > p_3$
对于第一种情况,$p1, p_2$ 的得分都可以是平局产生的,产生的方式是和 $p_3$ 对局,所以答案就是 $p_1 + p_2$。对于第二种情况 $p_1,p_2$ 不可能全部得分都来自于和 $p_3$ 的对局。所以,需要 $p_1$ 和 $p_2$ 对局产生一些平局的分数。通过分析可以得到 $p1 + p_2 – p_3$ 必为偶数,而且除以 2 以后必然小于 $p_1$。所以,将多余的分数用于 $p_1$ 和 $p_2$ 打平局是可能的。总结,所有分数都可以用来打平局,故答案是 $\frac{p_1 + p_2 + p_3}{2}$ 。
复杂度:时间复杂度 $O(1)$ ,空间复杂度 $O(1)$ 。
2 Cat, Fox and the Lonely Array
题目描述:
题目定义了一个概念,叫孤独数组 $A$ 。定义如下:
假设数组的长度为 $n$,如果
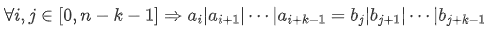
则我们称 $A$ 为 $k$ 维孤独数组。
现给出一个特殊构造的数组,要求找出该数组 $k$ 可以取的最小值。
数据范围:
$1 \le t \le 10^4$,$1 \le n \le 10^5$
解题思路:
看到这个数据范围,就需要考虑 $O(n \log n)$ 的算法了。对于位运算的题目,就要考虑位拆解求解。对于这种区间值的问题,可以先维护一个前缀和。由于是或运算,我们只需要维护区间内有无 1 出现就行。看到最小值,就可以考虑是否可以二分求解。
可以发现,如果该数组 $A$ 为 $k$ 维孤独数组,那么必然是 $k + 1$ 维孤独数组。证明如下:
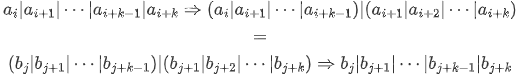
所以,二分解法是成立的。
复杂度:时间复杂度 $O(n \log n)$,空间复杂度 $O(n)$ 。