1 Guess the Maximum

题目描述：

给定一个数组 $A$ ，找到一个数 $x$ ，使得数组 $A$ 中所有长度大于 $2$ 的子数组 $A’$ 的最大值严格大于 $x$，求 $x$ 可取的最大值。

数据约束：

$2 \le n \le 5 \times 10^5$ ，$1 \le a_i \le 10^9$

解题思路：

找到所有长度等于 $2$ 的子数组的最大值的最小值 $m$ ，则 $x = m – 1$。

复杂度：时间复杂度 $O(n)$ ，空间复杂度 $O(n)$

2 XOR Sequences

题目描述：

给定两个数 $x, y$ ，现有两个无限长度的数组 $A, B$​ 。两个数组的构造方式如下：

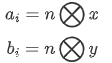
求这两个数组的公共最长字串的最大长度。

数据约束：

$1 \le x, y \le 10^9$

解题思路：

异或就是相同为 $0$ ，不同为 $1$ 。那么最长公共字串的长度就是 $x, y$ 相同最低为的长度所能表示的二进制数的最大值。

复杂度：时间复杂度 $O(\log x)$ ，空间复杂度 $O(1)$

3 Earning on Bets

题目描述：

给定一个数组 $K$ ，长度为 $n$ 。要求构造一个数组 $A$ ，长度同样为 $n$ 。我们定义 $S = \sum_{i=1}^{n} a_i$ ，现要求 $\forall i \in[1, n]$ ，都有 $a_i \times k_i > S$ 。请构造这样的一个数组 $A$ 。

数据约束：

$1 \le n \le 50$ ，$2 \le k \le 20$

解题思路：

我们假设一个数 $x$， 每个数 $a_i = \frac{x}{ki}$ ，那么我们只需要满足 $\sum{i = 1}^{n} \frac{x}{k_i} < x$ 即可，如果不能满足该不等式，就不存在这么一个数组 $A$ 。对于这个数 $x$ ，我们可以选择数组 $K$ 的最小公倍数。

复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$

4 Fixing a Binary String

题目描述：

给定两个数 $n, k$ ，并提供一个字符串 $S$ ，这个字符串仅有 $0, 1$ 组成，且长度为 $n$ 。现需要对数组进行一下操作：

• 选定一个数 $p$ ，将 $[1, p]$ 范围的字符串进行翻转（假设字符串的起始下标为 $1$ ），得到新的字符串 $S’$ 。
• 将 $S’$ 循环左移 $p$ 位，得到新的字符串 $S”$ 。

如果得到的字符串 $S”$ 满足以下条件：

• $s_1 = s_2 = \cdots = s_k$
• 对于 $\forall i \in [1, n – k]$ ，都有 $si \neq s{i + k}$

我们称这个字符串是符合要求的。

求满足要求的 $p$ 值。（有可能有多个值，只需要输出一种即可）

数据约束：

$1 \le k \le n$ ，$2 \le n \le 2 \times 10^5$

解题思路：

可以推导发现，最终生成的字符串的形式是以连续 $k$ 个的 $0, 1$ 交替出现的序列，最后一组不一定要满足 $k$ 个。

我们维护两个数组：$dp_l[0/1][i]$ 表示以 $i$ 位置结尾的以 $0, 1$ 结尾左侧满足上述条件的连续 $k$ 个的组数；$dp_r[0/1][i]$ 表示以 $i$ 位置结尾右侧以 $0, 1$ 结尾左侧满足上述条件的连续 $k$​ 个的组数。

遍历每一个位置 $p$ ，在右侧可以找到一个符合规定的最大长度，有可能会剩余一个不满足条件的子串，且这个子串长度必然小于 $k$ ，大于等于 $k$ 就不满足要求。既然长度不够，我们可以从 $p$ 的左侧借用一点子串来填充剩余部分。借用部分必须和剩余部分相同。

借用之后，我们在借用的左侧，寻找到最长符合要求的子串，此时也可能会剩余一个子串，且这个子串长度必然小于 $k$ ，大于等于 $k$ 就不满足要求。左侧剩余部分必须相同，且和符合部分进行有效衔接。

需要提升效率的地方就是查询这些符合规定的最大长度，此时就可以使用前面提到的 $dp$ 数组。又因为需要翻转，所以左侧是维护一个向左查询的数组，右侧是维护一个向右查询的数组，这就是为什么要两个 $dp$ 数组的原因。

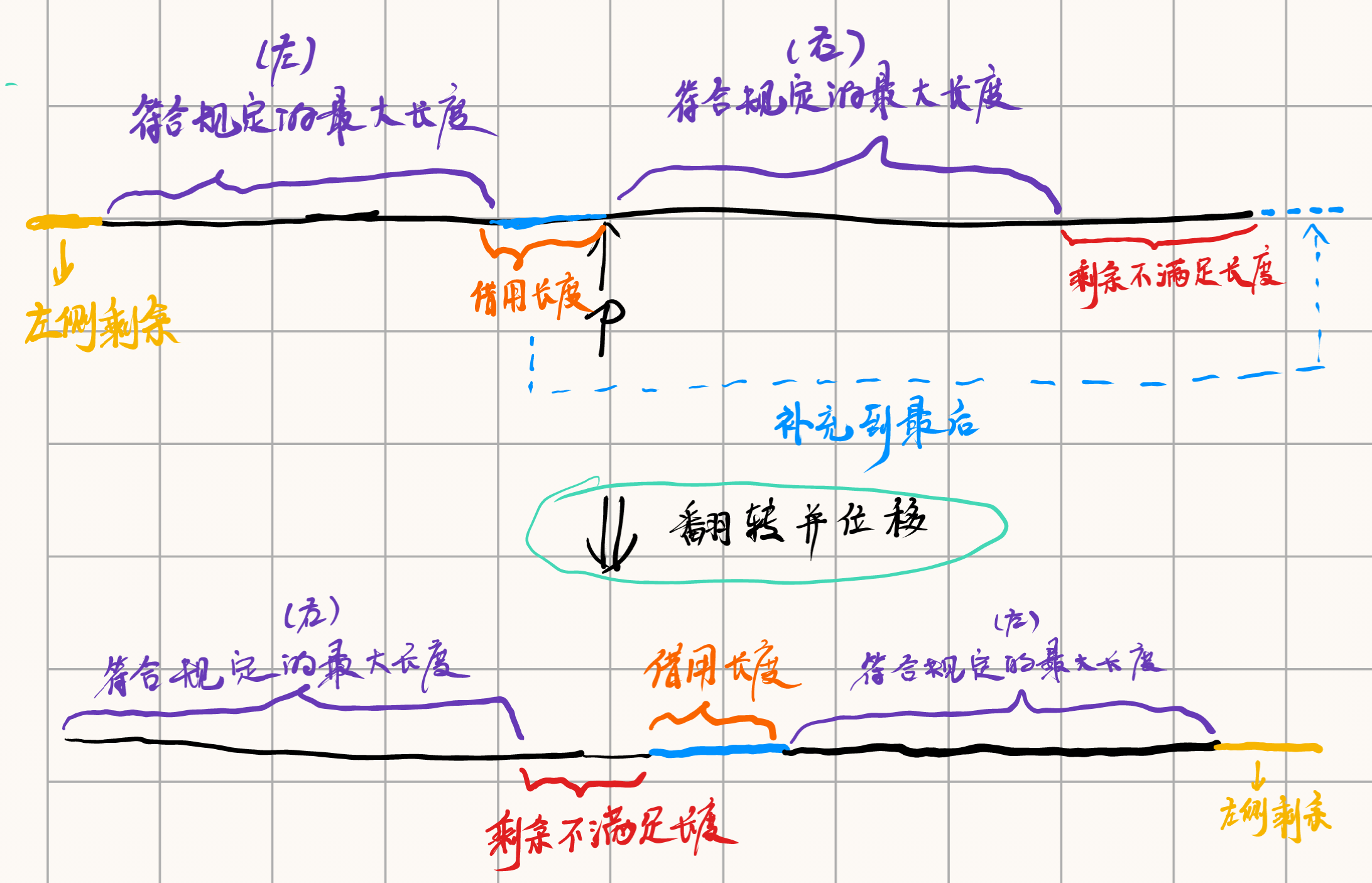
这个题目的细节非常的多，这里我主要是少考虑了这两种情况，右侧符合规定的最大长度为 $0$ ，以及 $k = n$ 的情况。

复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$