1 最长严格递增递减子数组

题目描述：返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。

数据约束：数组长度 $n \leq 50$。

解题思路：

遍历检查。维护两个数组，$incr[i]$ 表示以下标 $i$ 为结尾的最长严格递增的子数组；$desc[i]$ 表示以下标 $i$ 为结尾的最长严格递减子数组。转移公式如下：
$$
incr[i] = nums[i – 1] < nums[i] ? incr[i – 1] + 1 : 1
$$

$$
desc[i] = nums[i – 1] > nums[i] ? desc[i – 1] + 1 : 1
$$

最后答案为两个数组的最大值。

复杂度：时间复杂度 $O(n)$，空间复杂度 $O(n)$。

2 满足距离约束且字典序最小的字符串

题目描述：

给你一个字符串 s 和一个整数 k 。

定义函数 distance(s1, s2) ，用于衡量两个长度为 n 的字符串 s1 和 s2 之间的距离，即：

• 字符 'a' 到 'z' 按 循环 顺序排列，对于区间 [0, n - 1] 中的 i ，计算所有「 s1[i] 和 s2[i] 之间 最小距离」的 和 。

例如，distance("ab", "cd") == 4 ，且 distance("a", "z") == 1 。

你可以对字符串 s 执行 任意次 操作。在每次操作中，可以将 s 中的一个字母 改变 为 任意 其他小写英文字母。

返回一个字符串，表示在执行一些操作后你可以得到的 字典序最小 的字符串 t ，且满足 distance(s, t) <= k 。

数据约束：字符串长度 $n \leq 100$，$k \leq 200$​。

解题思路：

贪心策略，毕竟要字典序最小。从第一个字符开始，从字符 a 开始尝试直到剩余操作次数满足将该字符进行修改，满足就进入到原字符串的下一位，直到修改次数用完为止。

复杂度：时间复杂度度 $O(n)$，空间复杂度 $O(n)$。

3 使数组中位数等于 k 的最少操作数

题目描述：

给你一个整数数组 nums 和一个 非负 整数 k 。

一次操作中，你可以选择任一下标 i ，然后将 nums[i] 加 1 或者减 1 。

请你返回将 nums 中位数 变为 k 所需要的 最少 操作次数。

一个数组的 中位数 指的是数组按 非递减 顺序排序后最中间的元素。如果数组长度为偶数，我们选择中间两个数的较大值为中位数。

数据约束：

数组长度 $n \leq 2e^5$，数据大小在 32 位整型范围内，$k$ 在 32 位整型范围内。

解题思路：

既然要操作次数最小，那么就只需要修改原数组中位数附近的数即可，因为这些数也离中位数的差值最小了。要找原数组的中位数，就需要对原数组进行排序。

要使 $k$ 成为中位数，就需要在排序后的原数组中找到比 $k$ 大的数的下标位置，可能有以下两种情况：

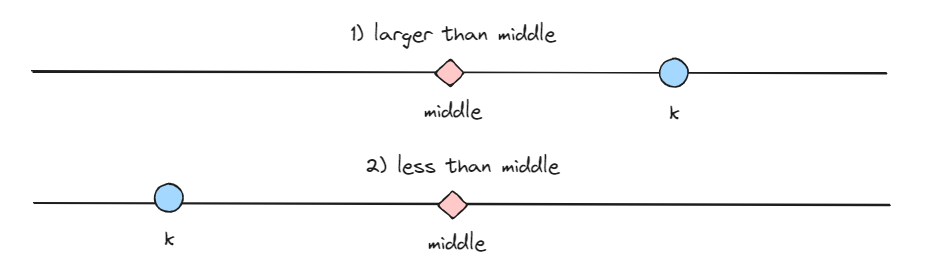
我们对其进行逐一讨论：

1. $k$ 在原中位数右侧，我们需要将 $middle -> k$ 这个区间的数都改成 $k$。操作之后，$k$ 右侧数都比 $k$ 大，不影响中位数，$middle$ 左侧的数都小于等于 $middle$，也不会影响中位数，这样中位数就是 $k$。
2. $k$ 在原中位数左侧，我们需要将 $k -> middle$ 这个区间的数都改成 $k$，这样中位数就是 $k$。

找到 $k$​ 的位置可以遍历也可以二分。

复杂度：时间复杂度 $O(n \log n)$，空间复杂度 $O(n)$。